LOADING...

加载过慢请开启缓存

loading

机器学习李宏毅-1

2023/12/23 Study

Regression (Example:Poke)

Step1:Model

  • y=b+w*x$_cp$ (weight/bias)
  • y=b+$\Sigma$$w_i$$x_i$ (各种不同的属性) (feature)

Step2:Goodness of Function

Training Data => ($x^n$,$y^n$)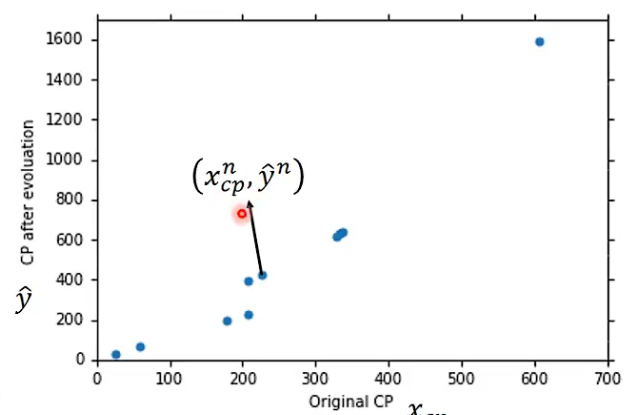
Pasted image 20231223145442.png

  • Loss function (func) :judge how bad the func is

  • L( f ) = L( w, b ) = $\Sigma$( ( $y^n$ - ( b + w*$x^n$ ) )$^2$

  • 计算估测误差值之和
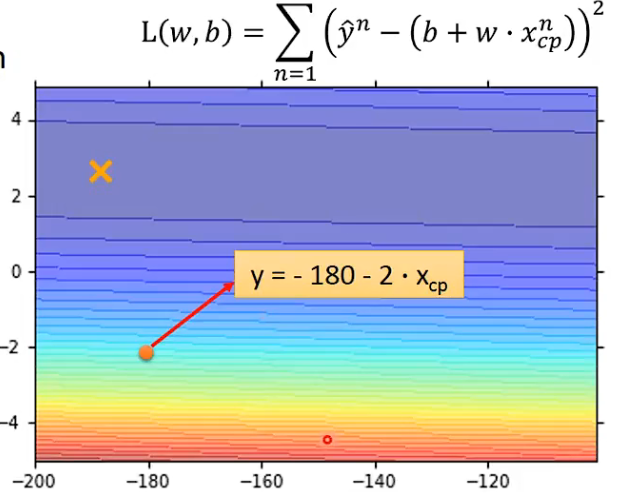
    Pasted image 20231223150232.png

  • Then Pick the Best Function

  • f$^*$ = arg min L(f) =>w$^*$,b$^*$

Step3:Gradient Descent

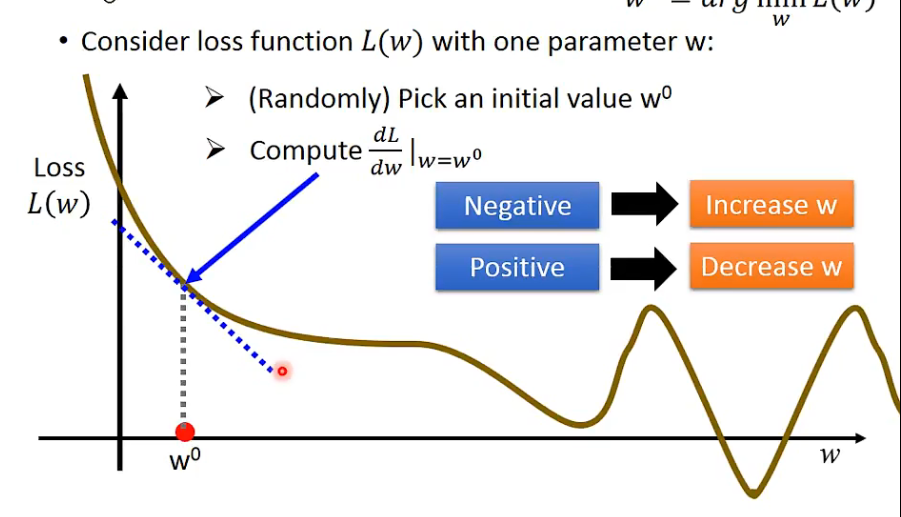
Pasted image 20231223151022.png

One parameter

  • Step Size : -$\eta$$\frac{dL}{dW}$|w=w$^0$
  • dL : 陡峭程度
  • $\eta$ : Learning Rate (学习速度)
  • …… Need Many Iteration
  • Final => Local optimal

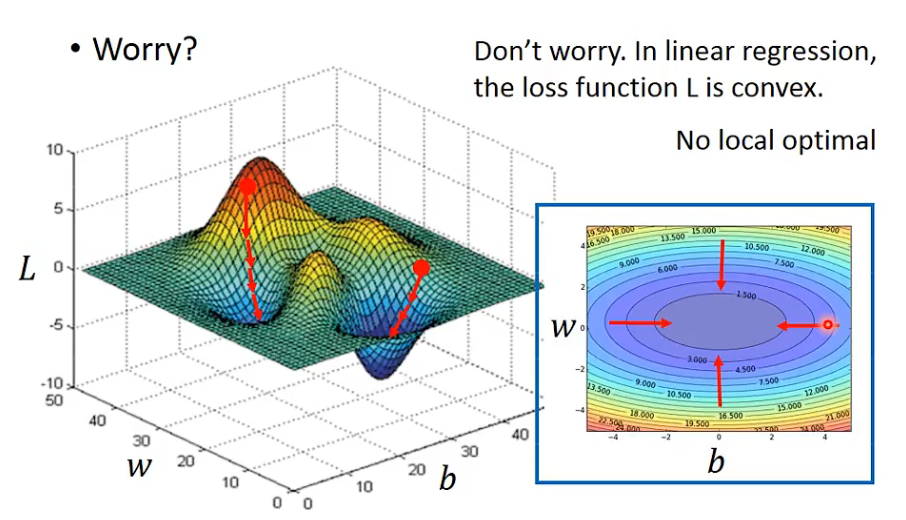
Two parameters

  • -$\eta$$\frac{dL}{dW}$|w=w$^0$ -$\eta$$\frac{dL}{db}$|b=b$^0$
  • w$^0$,b$^0$ => w$^1$,b$^1$
    Pasted image 20231223152409.png

Result

  • Error : $\Sigma$e$^n$ (e = y - $\hat{y}$ )
  • 一个x是一条直线，预测精度不够，需要一个更复杂的model
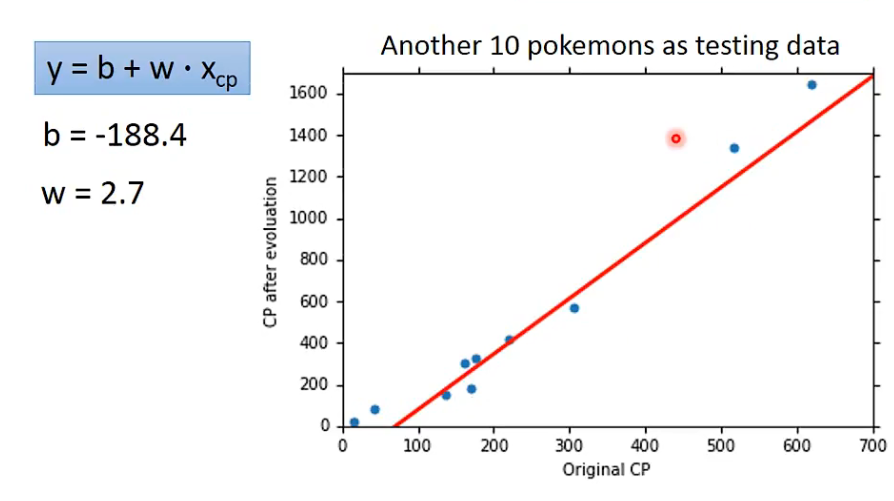
    Pasted image 20231223153736.png

Another Model

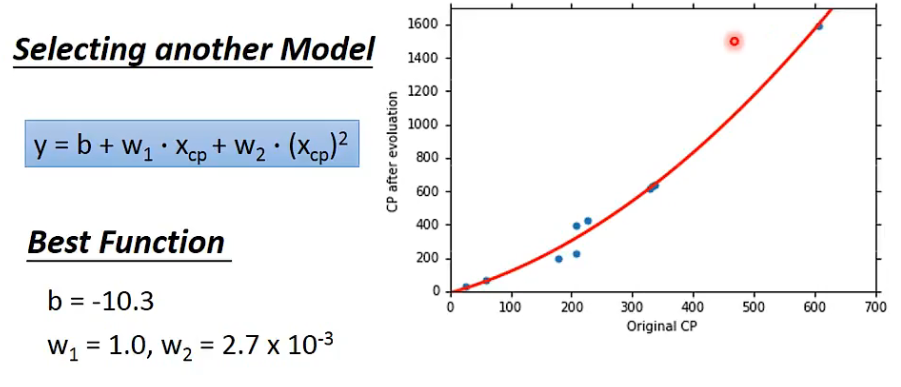
  • 考虑二次项的误差
    Pasted image 20231223153805.png

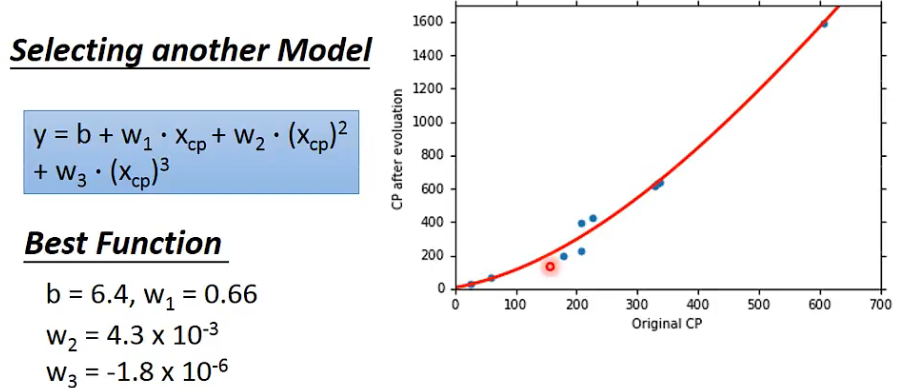
  • 考虑三次项的误差 (已经没有太大差别)
    Pasted image 20231223153946.png

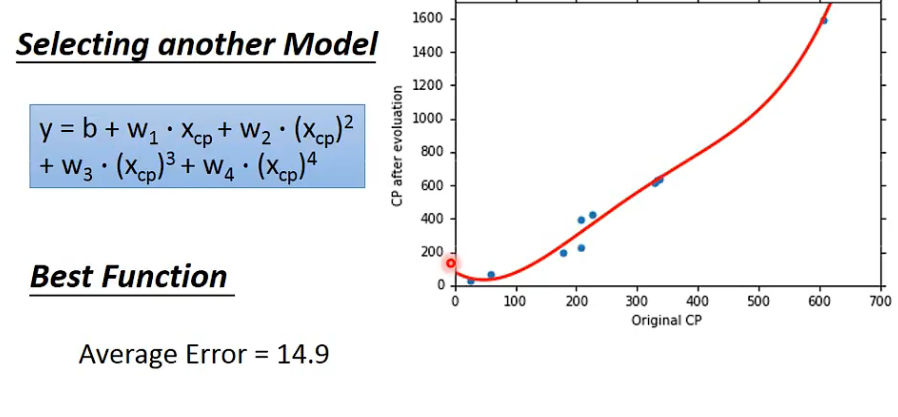
  • 考虑四次项 (误差反而变得更大了)
    Pasted image 20231223154159.png

  • 考虑五次项 (误差爆炸，寄)

Redesign the Model (Hidden Factors)

  • 以种族进行分类取得多组值，合并为一个Linear model
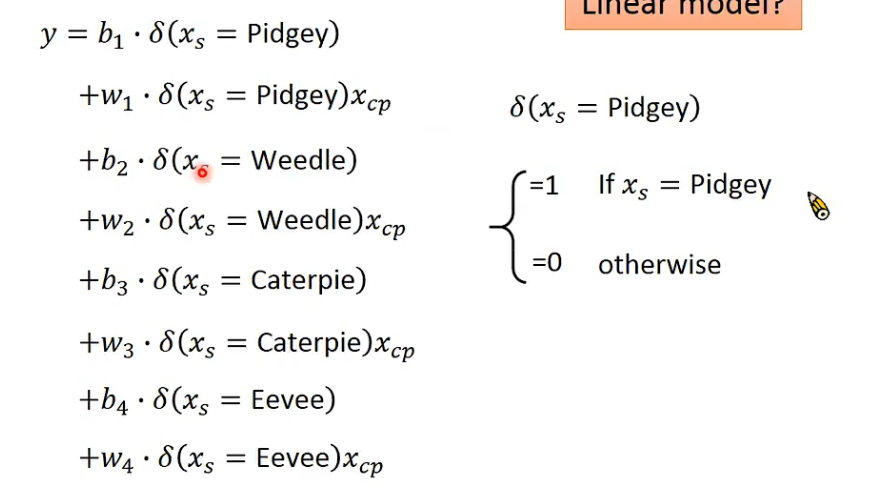
    Pasted image 20231223155323.png

  • 加入所有已知Factor

  • 反而Overfitting(过拟合),误差值很大
    Pasted image 20231223155943.png

Regularization

  • L( f ) = $\Sigma$( ( $y^n$ - ( b + w*$x^n$ ) )$^2$ + $\lambda$$\Sigma$(w$_i$)$^2$
  • 找到w的参数越小越好